Locating the Center of a Borderline Tree

By Ken Desmarais, Assistant District Ranger, White Mountain National Forest

 Timber cruisers utilizing angle count sampling (ACS) also known as horizontal point sampling or its variants are often required to check the distance from point center to the center of a borderline tree to determine if the tree is to be considered “In” or “Out”. The method used is to multiply the plot radius factor (PRF) by the tree’s diameter at breast height (DBH). Then this distance, the so-called “critical distance” is used as the maximum distance a tree’s center can be from the point center to be considered “In”. The tolerances of this measurement are somewhat precise, generally 0.1 to .01 feet in the United States. Although cruisers understand that the measurement is taken to the center of the tree, there is often disagreement where the center is actually located. This note is intended to help cruisers locate the center of the tree for the purposes of determining whether a tree is “In” or “Out”.

 Which “center” are we measuring to?

Cruisers often ask if the center is the pith of the tree. From the perspective of ACS, the biological center or pith, has no relevance. We are really concerned with the geometric center or centroid of the tree. In practice it is nearly impossible to measure to this centroid unless we cut down the tree. Our best effort is usually measuring the distance to a specific point on the side of the tree that is at right angles to the centroid. In other words we want our tape to brush along the side of the tree and where a right angle from the tape projects to the tree centroid, we want to measure the distance … sort of. Because the distance is calculated to the centroid and we must measure to the side of the stem, we set up a right triangle whose sides can be calculated using the Pythagorean Theorem

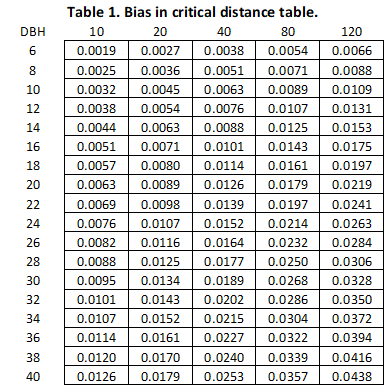
Where A is the length of the tape along the outside of the tree, B is the tree radius in feet (or half the DBH in feet) and C is the critical distance (or Plot Radius Factor x DBH). There is a slight bias here because if B is greater than zero then A must be less than C. This bias in A is less than 0.1 feet in general practice, for example, a 10 inch tree will give a 0.0045 foot bias using a 20 BAF. Using a standard critical distance table the cruiser will tend to measure a little further than he should.

 How big of a problem is this?

There are two questions being posed here; (1) where exactly is the location of the side of the tree that we should be measuring to, and (2) how big of a problem is it if we are using a standard critical distance table?

Locating the correct location - This author has been cruising timber for forty years. Over that time I have witnessed very animated discussions in the woods on a cruise point about the exact location to measure the tree center. Foresters often have very different understandings of where this location should be. I have also observed the tree center located in what seemed like a very cavalier manner. In a recent field exercise with some cruisers we located several borderline trees and measured out with the distance tape and marked our estimated tree center with permanent markers. Interestingly enough the distance between the closest and farthest marks were sometimes as much as 0.3 to 0.4 feet apart. This could easily fail a check cruiser’s inspection. The problem can be considerably more difficult with trees that are very irregularly shaped.

 How serious is the bias in critical distance tables? – Table 1 shows the difference between the critical distance and the proper distance to measure with a tape to the side of a borderline tree (line A). The difference increases with basal area factor. For trees 40 inches DBH or less the difference is less than 0.05 feet. To this author the bias is a very small problem because (1) it will effect a small number of trees and (2) there is bias already in play with trees that are not perfectly round cylinders. Grosenbaugh (1958) and Iles and Fall (1988) have addressed the non-round issues in detail already. On the other hand, in some shops, cruisers may be accountable for critical distance to a tolerance of 0.01 feet. Table 1 shows that the practical range of tree size and BAFs used in North America could easily exceed a tolerance of 0.01 feet. It is a small task to give cruisers better critical distance tables to work with in the field, however this distance tolerance can also be affected by things like a point center staff that is not exactly vertical.

How do we locate the tree center in practice?

Training may be the best solution to this problem. Cruisers generally hate carrying calipers in the woods, however calipers can be very useful in training a cruiser’s eye for spotting the center of the tree. Here is how that works. Place the caliper on the tree and aim the main beam (the part with the ruler on it) at the point center. Contract the caliper jaw until it is flush with the tree being measured. Next, read the diameter on the caliper. Half this diameter is the center or location to read the distance from the point center. In our field trial, practice with the caliper helped tremendously with narrowing the distance between the cruiser’s marks and the proper location for the center of the tree. After a small amount of practice a cruiser should be quite proficient without the need for carrying the calipers in the woods.

 Literature Cited

Grosenbaugh, L. R. 1958 “Point sampling and line sampling: Probability theory, geometric implications, synthesis”. Occasional paper 160, USDA Forest Service, Southern Forest Experiment Station.

Iles, Kim and Fall, Mike 1988 “Can an angle gauge really evaluate "borderline trees" accurately in variable plot sampling?” Canadian Journal of Forest Research, 1988, 18(6): 776-783, https://doi.org/10.1139/x88-118.