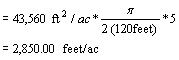Line Intersect Sampling: 

An example of computations other than volume.

Transect sampling is widely used to estimate down wood. It was developed to efficiently estimate volume (or weight) of coarse woody debris after logging and is almost always presented this way in textbooks and articles. Past articles in the Newsletter have presented the theory behind transect sampling (issue 21, page 1) and a simple example (issue 25, page 3).  

Often, however, we are interested in things other than the volume of logs per acre in a unit.  We may want to know the number of logs, the average size of logs, or the volume of logs in a particular decay class.  In this article we demonstrate how to use data from a transect sample to estimate values other than volume.  

Transect sampling, like Variable Plot sampling (also “angle count”, “prism” or “Bitterlich” sampling) is a probability sample.  In Variable Plot sampling, trees are selected with probability proportional to basal area so that smaller trees represent more trees per area than larger trees.  With transect sampling logs are selected with a probability proportional to their length so that shorter pieces represent more pieces per area than longer pieces.  Knowing this we can compute an expansion factor (the number of pieces per acre a specific log represents) for logs using transect sampling just as we would for other kinds of sampling (number of trees per acre a sample tree represents, also called a stand table factor).  For transect sampling this expansion factor is: 

 where 43,560 is the square feet in an acre, p is 3.14159, L is the length of the transect in feet and l_i is the length of a specific log in feet.  For example, if we had a transect of 120 feet and a piece that intersected along a transect that was 15 feet long, then that piece would represent 38.0 pieces per acre.  If one was doing this in metric, L and l_i would be in meters and 43,560 would be replaced with 10,000 m²/ha.  The nice thing about this expansion factor is that it expands everything about the log.  The problem with it is that you have to know the length of the log (Before you give up, remember in angle count sampling you have to know tree diameter to get trees per acre). 

Using this idea of an expansion factor we can now compute any per acre estimate by multiplying that attribute by the expansion factor per acre (or hectare) for each log.  If we designate something we want to know about the logs in a stand as x, we can compute the per acre estimate 

 from: 

where x_i and l_i are the attribute of interest on the log and length of each of the (i) intersected pieces on a transect.  The value of x_i/ l_i is summed for all logs crossed by the transect.  If multiple transects were measured in an area, one would have to divide the answer from above by the number of transects to get the average.  

Now you might remember from the previous articles or from doing transect sampling that you did not need the log length to get volume.  This is true because if x_i were log volume it would be estimated from d_i2* l_i or diameter squared (cross-section area of the log) and log length. When we combine terms, note that the log lengths cancel (and we convert diameters to a radius to compute area in square feet) and we have: 

which is the formula most often seen in textbooks and articles on transect sampling. Note that in this case, d_i (in feet) is the minimum diameter of the log as you cross the centerline (at right angles to the centerline).  The article in issue 21 discusses this measurement short cut in more detail. 

Given the example used in issue 25 with a 120-foot transect and 5 logs intersected by the transect: 

  What is the total length of logs per acre?  This is kind of a trick question because in our formula above, x_i is the length of each log so that the log lengths cancel and we can get total length from a count of the intersecting logs (sound a little like getting basal area from tree counts?).  

 How many logs per acre are there? In this case x_i is 1.0 so we just have to sum up 1.0/l_i for all the logs (i.e. sum up the expansion factors): 

You could compute the average log size by dividing the volume per acre by the number of logs or the average log length by dividing the total length by the number of pieces.  In this example from issue 25, the total volume was calculated as 4,507 ft³/ac so our estimate of average log volume would be 4,507/472 = 9.55 ft³ or 2850/472 = 6.0 ft. 

If you had classified the logs by decay class or whether they were merchantable or not, one could find the number of logs in each class by doing the above calculations for only those logs which intersected the transect and were in the class of interest (just like creating a stand table in angle count sampling). 

If you were interested in estimating how many logs met a certain merchantability standard based a minimum piece diameter and length, you would have to measure the lengths of the logs that were intersected and had diameters at the small end of the log greater than the minimum required. 

One interesting question that will comes up when one begins collecting data in the field to compute expansion factors for transects is, what is the length of the log? Length is obvious for nice straight logs, but is not so obvious for logs that are forked or other strange shapes. Our advice on this is to measure piece length as the straight line distance along the piece you measured where it would have been included on the transect counts.   

We hope with this example it is clear that with a transect sample, estimates can be computed for any attribute on logs that are crossed by a transect.  

Errata: In preparing this article we ran across an error in the example of line intersect sampling presented in issue 25. The example begins with a transect with a length of 30 feet but the numbers in the example are worked out for a transect of length 120 feet. The 120 foot transect is the correct one.