A Plantation Problem from New ZealandIn some ways, New Zealand has simple inventory issues. Many of the stands are plantations with known ages, so drilling trees is not necessary. There is generally only one species in each stand, and very few species (unlike the blizzard of hardwoods that some folks are faced with). The environmental movement is only at the early stages of cramping and complicating the process. On the other hand, the slopes and the brush can be as nasty as many places in the Pacific Northwest (you’ve seen The Lord of the Rings – right?) The introduced species of underbrush are as vigorous as the introduced species of crop trees. Moving around in gorse or blackberries is as painful and expensive anywhere in the world. One of the problems that is exactly the same is the issue of sample size. How much of each kind of item do you need to measure? As always, the issue is balance in the sample design and practicality in the field work. How do you look at a complicated issue like the number of samples for stand value, or grade volume? Here are two ways :
The STAR_BAR spreadsheet that many of you use can balance the number of trees you count and measure, and that is quite useful. This is especially true when the question involves something about individual trees. Suppose we are concerned with the value of a stand we are selling. We need data. At this point Gerard Lynch, of Blakely Pacific company in New Zealand dug into his compilation program and made it print out the volumes, by log, in each tree from one of his Radiata pine cruises. We could then assign values to each log and do some analysis. Gerard, and Mike Buchanan of Blakely Pacific were kind enough to allow us to use this data as an example. We randomized the data and started looking at the answers as trees were added to the sample (this simulates an actual sampling situation).
You can see that we need very few trees in this plantation to get a good stand value. The CV of the $BAR is about 28% (similar to the CV for basal area). For VBAR the CV was only about 17%. We have larger CVs in the Northwest, but a similar relationship between the variability of volumes and dollars. If you enter this data into the spreadsheet STAR_BAR it will tell you how many trees to measure and count for any given SE%.
You can use such a graph to decide the number of trees that will stabilize answers for particular grades You still need to do enough counts to expand those tree answers to total volume or total value per acre.
|
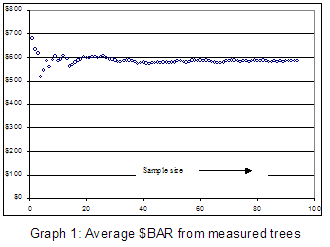 The
graph of the average value after you add each tree measurement ($BAR is the
tree value ¸ tree basal area) appears at right. The stand, in other words,
is worth about $600 for every square meter of basal area in the stand. The
variability (CV) of basal area was about the same. We get basal area by
counting trees, of course.
The
graph of the average value after you add each tree measurement ($BAR is the
tree value ¸ tree basal area) appears at right. The stand, in other words,
is worth about $600 for every square meter of basal area in the stand. The
variability (CV) of basal area was about the same. We get basal area by
counting trees, of course.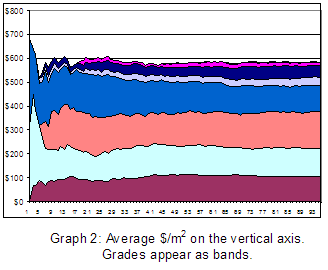 How
about grade values? What if some measurements offset others? In a given
tree, for instance, if one grade has more volume then less can occur in the
other grades. Graph #1 was the result when we combined their values. How
about individual grades? We could calculate individual CVs, but a simple
graph might be useful. Let’s look at the averages for {$grade/BAR} as
trees are added to the sample (not all trees will have each grade in them,
making this quite variable). You can either look at all of them combined
(graph #2), or individual grades (graph #3 – which shows only 3 of the
many possible grades, for printing clarity).
How
about grade values? What if some measurements offset others? In a given
tree, for instance, if one grade has more volume then less can occur in the
other grades. Graph #1 was the result when we combined their values. How
about individual grades? We could calculate individual CVs, but a simple
graph might be useful. Let’s look at the averages for {$grade/BAR} as
trees are added to the sample (not all trees will have each grade in them,
making this quite variable). You can either look at all of them combined
(graph #2), or individual grades (graph #3 – which shows only 3 of the
many possible grades, for printing clarity).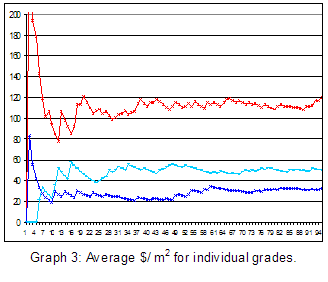 According
to the CVs from this actual cruise data, the number of count plots should be
about the same as the number of trees measured. This is because the CV of
basal area was about the same as the CV of $/m2 (or $/ft2).
According
to the CVs from this actual cruise data, the number of count plots should be
about the same as the number of trees measured. This is because the CV of
basal area was about the same as the CV of $/m2 (or $/ft2).