by Kim Iles
The sampling error you calculate (and what affects it) has a great influence on the cost of your inventory. This is a suggestion for a different way to do the field work. If you want to, you can skip this history section.
The first Variable Plots measured every tree on every sample point, and therefore gave a volume at every location. The statistics were simple and traditional. They used the formula for a simple random sample (#1, below), just like the one used for Fixed Plot Sampling. Everyone was comfortable with that, although it was wrong.
The random sample formula is not right for systematic samples (Variable or Fixed Plots) because it overstates the sampling error (increasing the number of plots) - but it is almost always used. The computation of sampling errors for systematic samples can often be done, at least approximately, but nobody seems to make the effort.
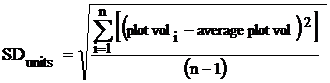 Stand
volume/acre
= The simple average of volume per acre on all plots.
Stand
volume/acre
= The simple average of volume per acre on all plots.
(#1) Statistics formula
 where
“n” is the number of plots taken.
where
“n” is the number of plots taken.
A big change came in about 1950 with the introduction of “Count Plots” by the consulting company of Mason, Bruce and Girard. They used the statistics for a “Double Sample”, which is one way to correct an estimate that you have at every sample point. Often, that estimate is in the “wrong” units. In this case every plot had a basal area estimated in square feet/acre by just counting trees. Some of these points (called “Measure Plots”) determined the timber volume in the units you wanted (BF or cubic, for instance) as well as the basal area. Because of the selection method, you totaled up all the Measured Plot volumes and divided by their total basal area. This is called a “Ratio of Totals”, or a “Ratio of Averages” method. With this ratio, you could then correct all the basal areas to get a volume at each sample point. That was also useful, because you could see the trend of volumes across the land base, even for the Count Plots.
The statistical formula typically stated is indecipherable, although Johnson’s USFS paper shows a pretty good one. This is because it is often corrupted from its logical form to make the hand calculation easy (not an issue since the 1960’s, really) so the logic cannot be seen. I have always avoided using Johnson’s Formula, but some people like it for their computations. The British Columbia Forest Ministry, for instance, still insists on using it for their timber cruising.
There are two parts to it – (A) How well you know the Basal Area of the stand? (from count plots), and (B) how well you know the conversion from basal area to volume (from the Measured Plots)? Let’s skip the ugly statistical equations and concentrate on the basic idea.
The stand volume can be expressed this way:
Volume = (Average Basal Area per acre) * (Total plot volumes / Total plot BA).
The first term is BA/acre for all plots, the second term is only for measured plots.
This is the same result as using the average VBAR ratio for the measured plots applied individually to the basal area for every one of the plots, then added up.
(#2) Statistics Formula : The statistical calculations are very messy1.
The US Forest Service was not initially sure about the right statistics when “Count Plots” were introduced. The sample average was obvious, but not the other statistics – because the trees were measured in “clusters” of several trees at each sample point. Could the method use the variability of volume/BA for individual trees, or must the cluster answers be used ? There are times when this makes a difference, although in forestry the trees can be reasonably considered as “independent” of each other when they are about the same height. Because of letters I have from the people involved, I believe that I have been able to trace the situation.
Floyd Johnson asked Lew Grosenbaugh what to do. They both worked for the USFS. Floyd probably knew already, but Lew was “the guy to check with” on statistical issues. Lew immediately recognized Count/Measure plots as a classic “Double Sample” and suggested the classic formula, which in forestry is known as “Johnson’s Formula” (because Johnson published a paper about it). I am sure Floyd would never name it after himself, which would be tacky, but names do often get attached to formulas.
A bit later, Dave Bruce (who introduced the wedge prism) took a different view. He suggested that you use a “Product Formula”, meaning that two separate averages are multiplied by each other. The average Basal Area (however you get it) is multiplied by the average Volume/BA ratio (however you get it) to give the volume/acre. The statistics are then computed with this very simple formula :
Volume/acre = [ average Basal Area/acre * (average tree VBAR from all trees) ]
The individual tree VBARs are averaged because they were selected with a prism.
(#3) Statistics Formula : First, compute the standard Sampling Errors in percent for Tree Count on the plots, and the Sampling Error in percent for all the tree VBARs.
![]()
This formula assumes that the tree VBARs are not correlated with the tree count or with each other at a sample point. The correct sampling error formula also has a very small 3rd term, which was dropped, and statistical formula (#3) became known as “Bruce’s Formula” in forestry – although it was clearly invented many years ago in the statistics field. We are now working with the VBAR on individual trees regardless of the plot they fell on. People now started to think about the averages and variabilities of Basal Area and VBAR as separate issues. As usual, “divide and conquer” methods increased efficiency.
This separation of the two parts eventually led to the Big BAF method (and similar ways to subsample for VBAR), which was not developed until about 19802. It makes sense to measure fewer trees more carefully (reducing measurement bias) if it does not hurt the precision of the cruise very much. It also makes sense to spread the tree measurements more evenly throughout the stand. Some of the time saved can also be put into additional Count Plots, which are typically the most variable part of any cruise.
Historically, you needed to measure a lot of trees if you did not want the “Measure Plots” to get too far apart. We still measure far to many trees in North America for this reason. Something was needed to reduce this large number of measured trees, because the VBARs are not that variable (compared to the tree counts). Big BAF was one of those solutions, and this short article will introduce another method.
When both apply, the Johnson and Bruce formulas give you the same volume, but slightly different statistics. Lew Grosenbaugh never liked the use of Bruce’s method because the statistics were not exactly right when trees are measured in clusters and at the same place as the Basal Area counts. Lew hated getting snotty notes from rookie university statisticians on trivial issues like this, and it was too expensive to do the research to prove that it was OK on a practical level. Lew did not like the use of Count Plots either. He probably thought it was too much to introduce at one time – and Variable Plot had just arrived in North America. In 1950, the psychology was wrong. Measuring all trees on all plots would feel more comfortable to new users of the Variable Plot method, because it would feel like the Fixed Plots they already used.
---------------------------------
Now to the new approach. Is it possible to do traditional and clearly correct Double Sampling and measure fewer trees? Yes, it is. You still need a way to calculate the volume on some plots (let’s call these “Thinned” Measure Plots) because only some of the trees will be measured. You then use the classic “Johnson Method” statistics of Double Sampling (Formula #2). It will be the same logic, based on an estimated volume for each measured plot.
How will we get this volume at each Thinned Measure Plot? For each plot, you need to choose one or more trees from each species to get a VBAR. As an example, let’s choose one tree from each species. I can think of ways to do that randomly, and so could you. Just make sure that the trees are chosen correctly3. This makes sure that for every Thinned Measure Plot we have an individual plot volume by species, except when the tree count is zero. This avoids the nasty problem of a Basal Area with no way of estimating volume at that measured plot.
In this case, the single selected tree represents the VBAR for the total number of trees of the species at that point. If one tree is chosen from 5, it represents all 5 of those trees. Here is a simple example in cubic feet per square foot for sample trees. Each species can be done individually, so you get total and species volumes for the plot.
EXAMPLE : 20 BAF prism
| Plot 1) | 1 fir : VBAR = 30 from 6 fir = | volume of [20BAF*30*6] | = 3,600 ft3 / acre fir |
|
Plot 2) |
1 pine : VBAR = 40 from 3 pine = | volume of [20BAF*40*3] | = 2,400 ft3 / acre pine |
| Plot 3) | 1 fir : VBAR = 50 from 1 fir = | volume of [20BAF*50*1] | = 1,000 ft3 / acre fir |
|
1 pine : VBAR = 40 from 3 pine = |
volume of [20BAF*40*3] | = 2,400 ft3 / acre pine | |
| = 3,400 ft3 / acre |
(if there are no trees on the plot, the plot gets a Volume and Basal Area of zero).
You can use any “measurement per square foot”, of course, for a VBAR of sample trees.
At this point, we are right back to the 1950s and can use Johnson’s statistical calculations because we now have a traditional “Double Sample”. The advantage is that we only measure some of the trees on each “Thinned Measure Plot”. Count plots continue to only count trees by species. When count plots are used, you will always have to contend with the problem of “orphan species”4 (more on that shortly). If we wanted to measure 2 trees out of 5 on the measure plots, we could multiply the average of those two VBARs by 5. The calculated Sampling Error is expected to be slightly larger than measuring all the trees at a point, of course, but the work is much faster.
To avoid changing any computer code or field inputs for volume calculation and statistics, use one tree for each species. If you have 5 of that species, duplicate that tree 5 times in the plot data. This is also a good way to test the method on data you already have available, and no computer problems should arise (unless you have edit programs that have a fatal error when you have several identical trees). It’s always good to have a method that will not cause additional computer or data entry problems. In general, no computer code should need to be changed. All reasonable compilation routines allow for weighting trees – often because of edge correction methods.
If you like, you can make all your plots into “Thinned Measure Plots” and the sample points all have individual volumes (so we use equation #1), which is very close to a Fixed Plot Sample process5. This similar “look and feel” to Fixed Plots might make it easier to sell to specialists outside forestry who think that Variable Plot Sampling is witchcraft. The measured number of trees is not far from Big BAF sampling, although it will be slightly less efficient (or so I believe), especially in mixed stands.
While I still believe that Bruce’s method is the most flexible and forward-looking way to sample (coupled with Big BAF or some other way to subsample for VBAR) this simple adaptation might be of interest to particular groups. The method generalizes to many other uses of Double Sampling, and I am not aware that it has been suggested before – at least in the forestry literature.
[1] If you care, contact me and I will send you a spreadsheet for it (email : kiles@island.net) or see chapter 53 of The Retread, The Reject and the Tower Statistician, which also has the spreadsheet on the DVD.
[2] Although Grosenbaugh considered that idea long ago.
[3] We have discussed the perils of choosing the nearest tree, or the first tree from North, in other articles.
I would suggest using a randomized list of numbers 1-15 (or whatever the largest tree count would be). Use a new list at each plot.
[4] Personally, I am happy to measure the first of any species encountered, and that measurement is put aside in case a VBAR is needed and that species never shows up on a measure plot. The chance of this is small, and any bias involved is very tiny indeed.
[5] This entirely avoids the issue of “orphan species” where you have a species on a count plot that never occurs on a measured plot.